plot(beef.data)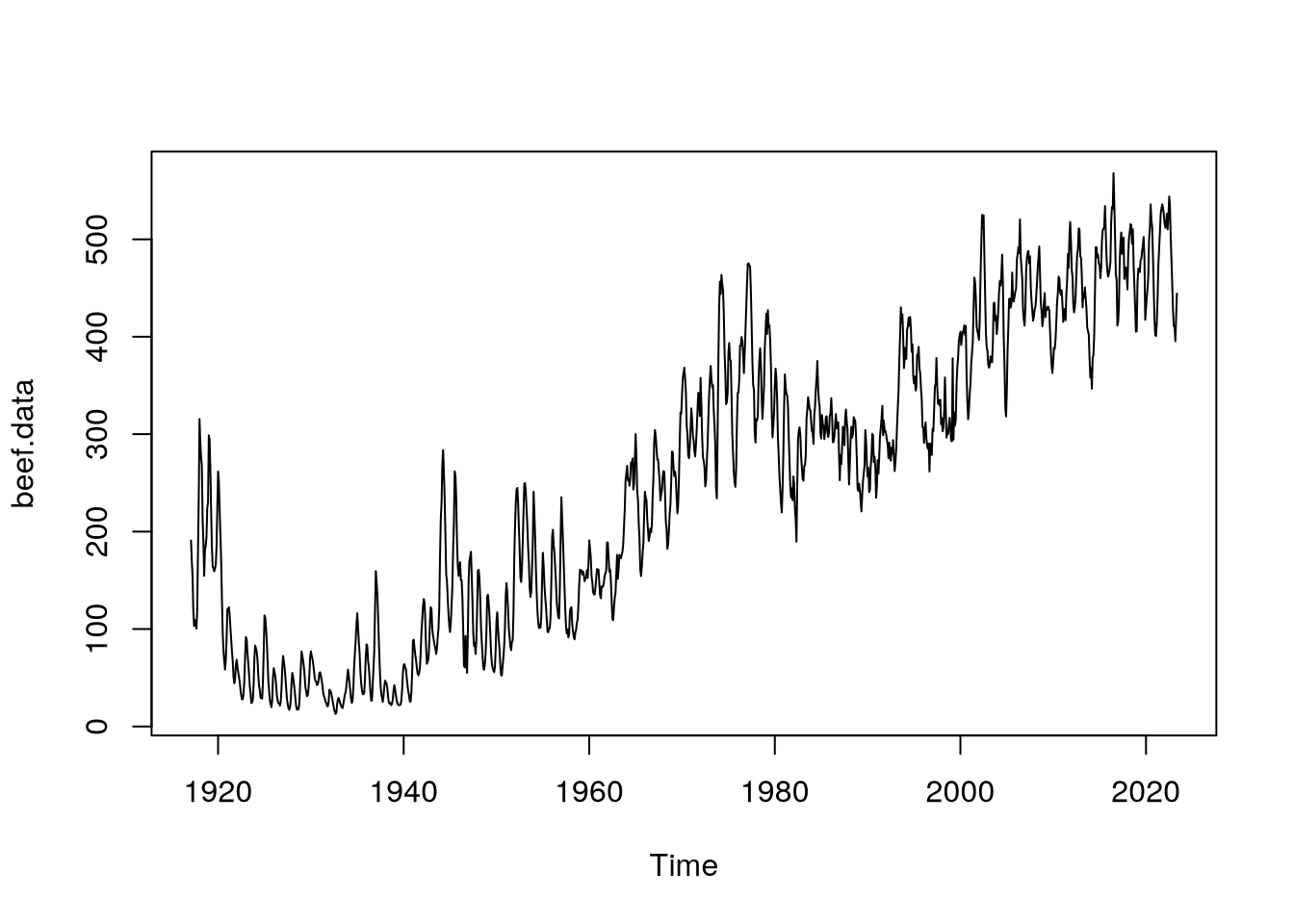
%#TODO
% Basic notation - general % Special symbols % Basic functions %image %cardinality % Operators - Analysis % Linear algebra % Linear algebra - Matrices % Statistics %at time % Game Theory % Optimization % Useful commands$$
Cílem projektu do předmětu M9121 Časové řady I bylo analyzovat námi vybraná data, která je možná chápat jako jednorozměrnou časovou řadu. Tuto časovou řadu zkusíme prozkoumat, pochopit, popsat její trendovou a sezónní složku a následně vytvořit model, který by šlo použít k predikci.
Data, která budeme analyzovat, pocházejí z webových stránek ministerstva zemědělství Spojených států amerických, viz U.S. Department of Agriculture (2023). Jedná se o množství hovězího masa (v milionech liber) uskladněného ve veřejných a soukromých chladírenských skladech (cold storage stocks). Konkrétně se bavíme o měsíčních údajích od února 1917 do listopadu 2023, máme tedy k dispozici 1276 pozorování.
V našich datech se nevyskytují žádná chybějící pozorování.
Data jsou ve formě excelového souboru, bylo třeba importovat je do R a převést do formy časové řady. Tyto úpravy jsme provedli následujícími příkazy:
nejprve jsme načetli data ze zmiňovaného excelového souboru pomocí knihovny readxl:
data <- read_excel("./MeatStatsFull.xlsx",
sheet = "ColdStorage-Full",
skip = 1)dále jsme odstranili nepotřebné řádky, které obsahovali pouze textové informace o datech:
data <- data[-c(1277:1281), ]pokračovali jsme vypsáním datumů měření množství hovězího masa
times <- rev(data$`Meat 1/`)z čehož jsme si potom vytvořili časová data pro vytvoření časové řady
month <- 1/12
times.num <- seq(from = 1917 + month,
by = month,
length.out = length(times))nakonec jsme vybraná data seřadili “v čase dopředu”
beef <- rev(data$Beef)a převedli je do časové řady
beef.data <- ts(beef,
start = times.num[1],
end = times.num[length(times.num)],
frequency = 12,
deltat = month)Po vykreslení dat již ve formě časové řady (obrázek) zjistíme, že rozptyl se v čase nemění, není proto třeba provádět logaritmickou transformaci dat.
plot(beef.data)
Tento krok jsme si zdůvodnili i po vykreslení grafu klouzavé směrodatné odchylky, která se zdá být v čase konstantní.
plot(rollapply(beef.data,
width = 12,
FUN = sd))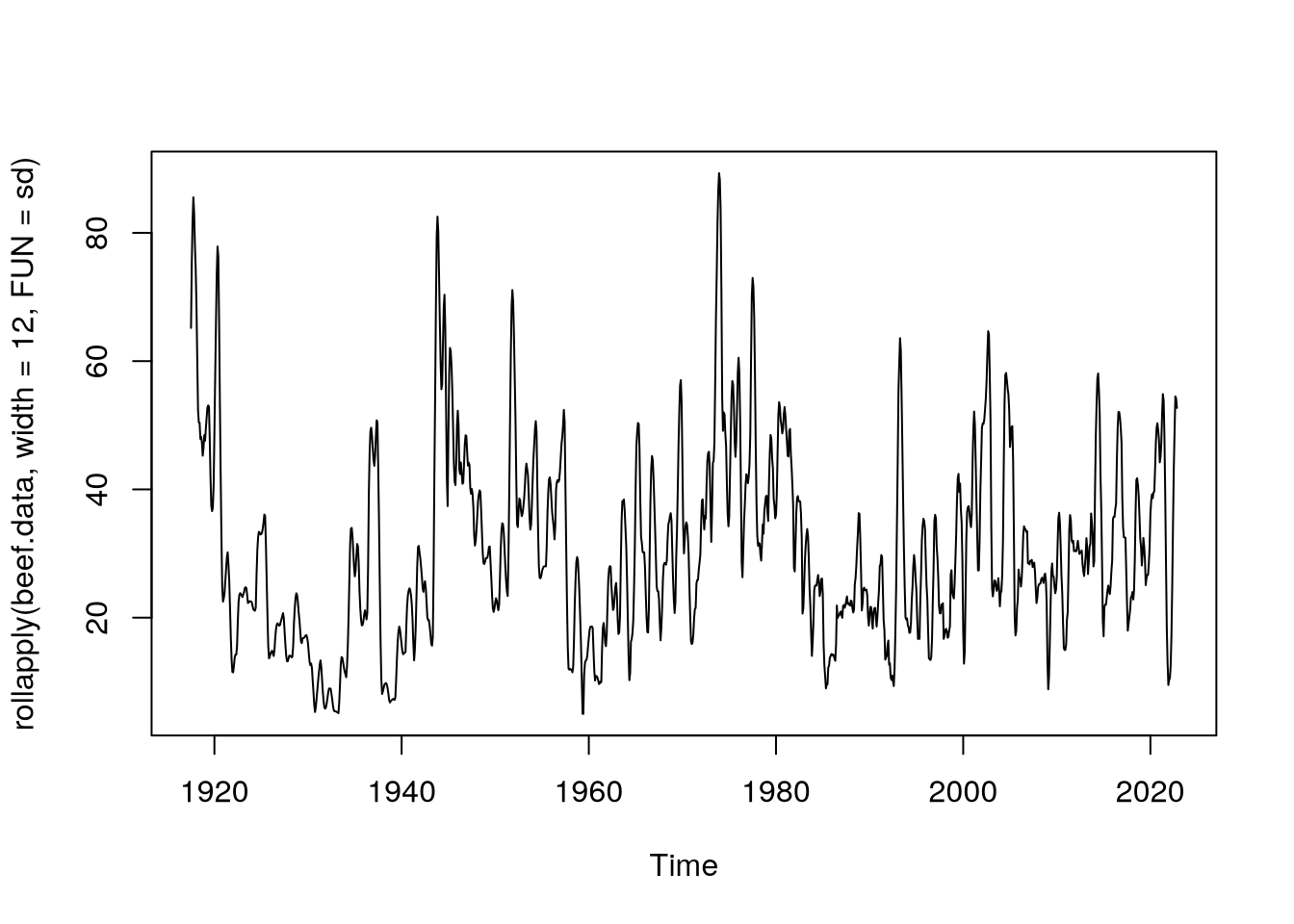
Naše časová řada ovšem není stacionární, neboť se v čase mění její průměr. Toho si můžeme všimnout po vykreslení funkce klouzavého průměru:
plot(rollapply(beef.data,
width = 12,
FUN = mean))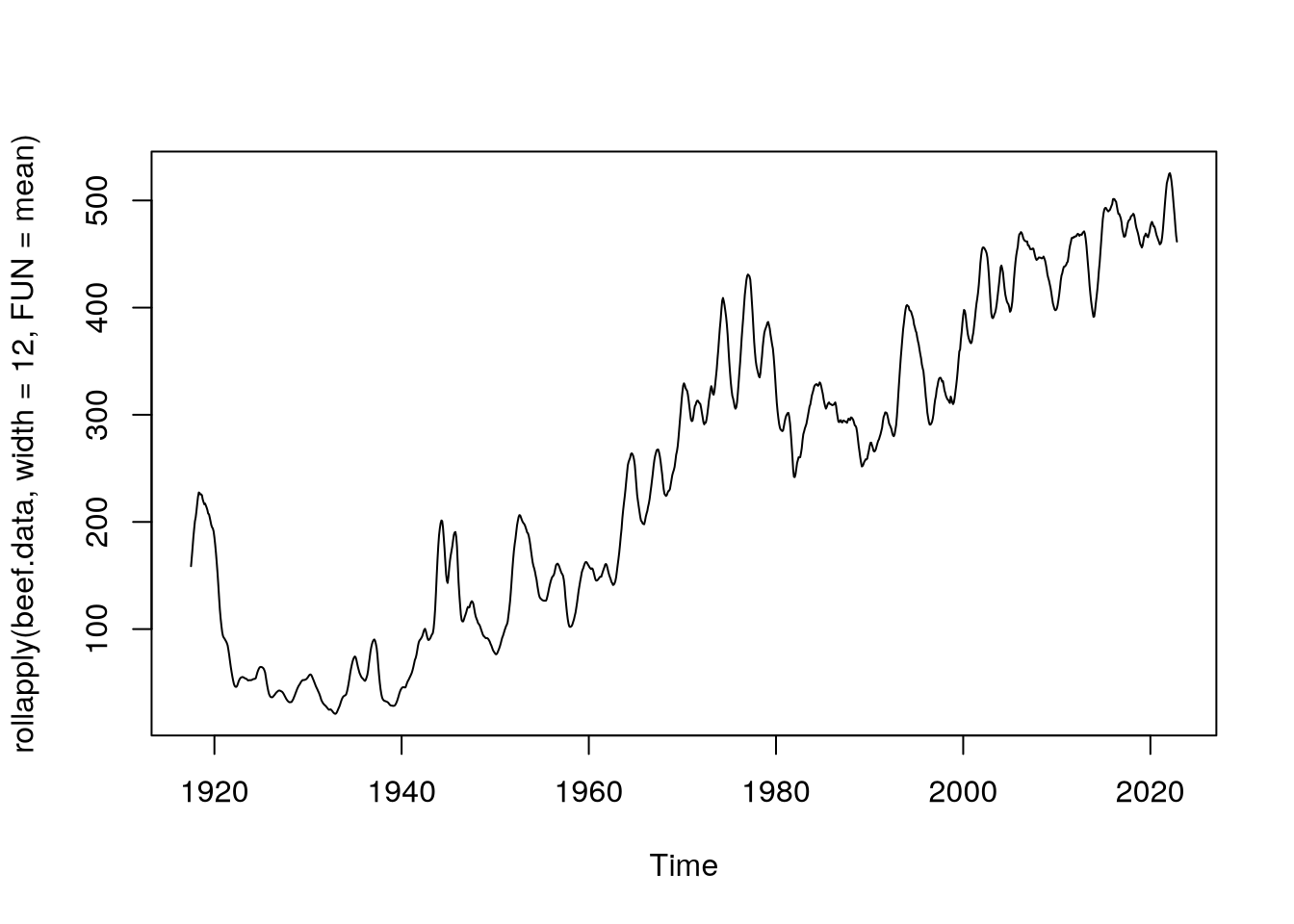
Po prvotním vizuálním prozkoumání časové řady můžeme přistoupit k transformaci dat za účelem získání nové, stacionární časové řady, na které budeme moct provádět další úpravy.
beef.diff <- diff(beef.data,
lag = 1)
plot(beef.diff)
acf(beef.diff)
pacf(beef.diff)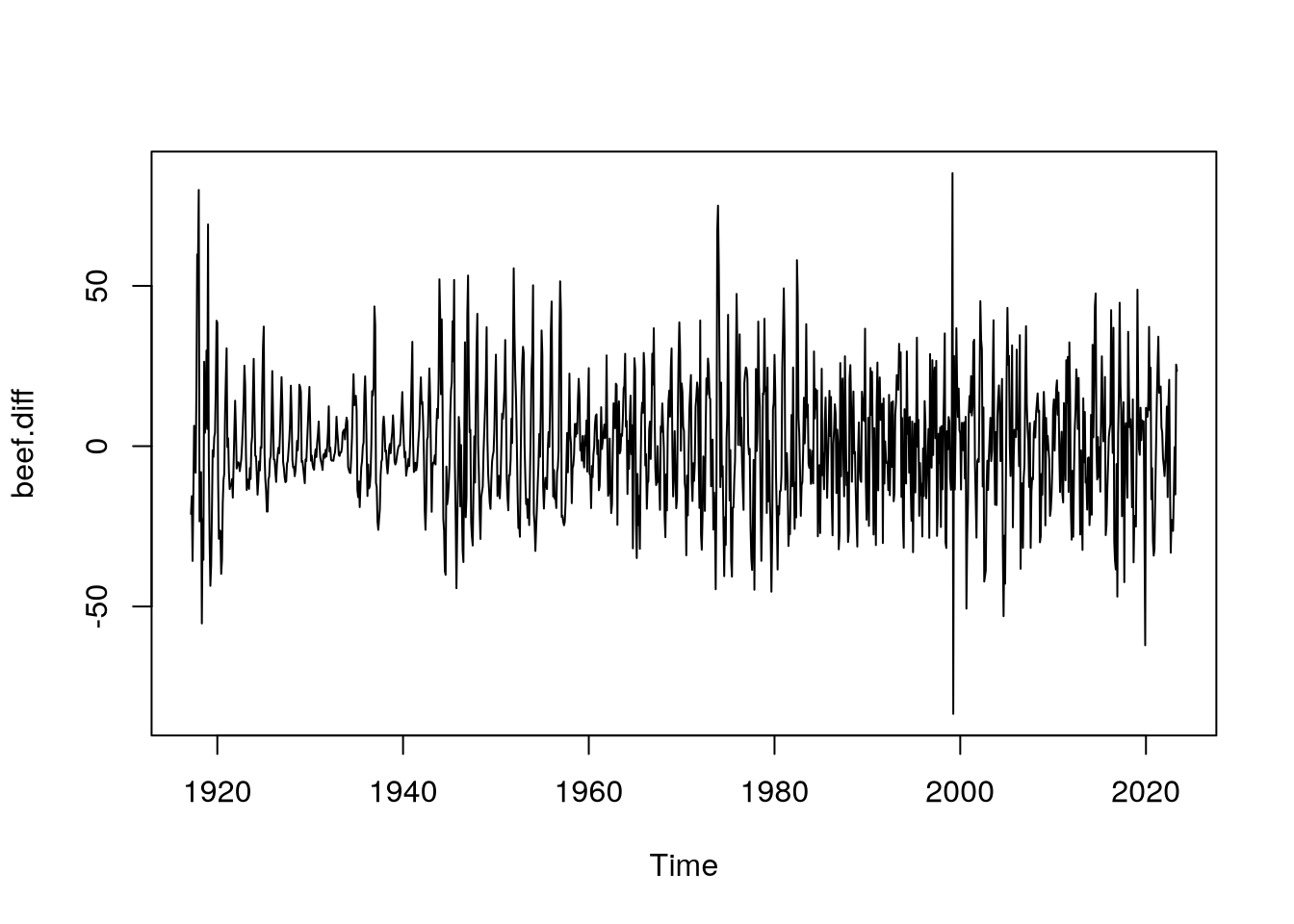
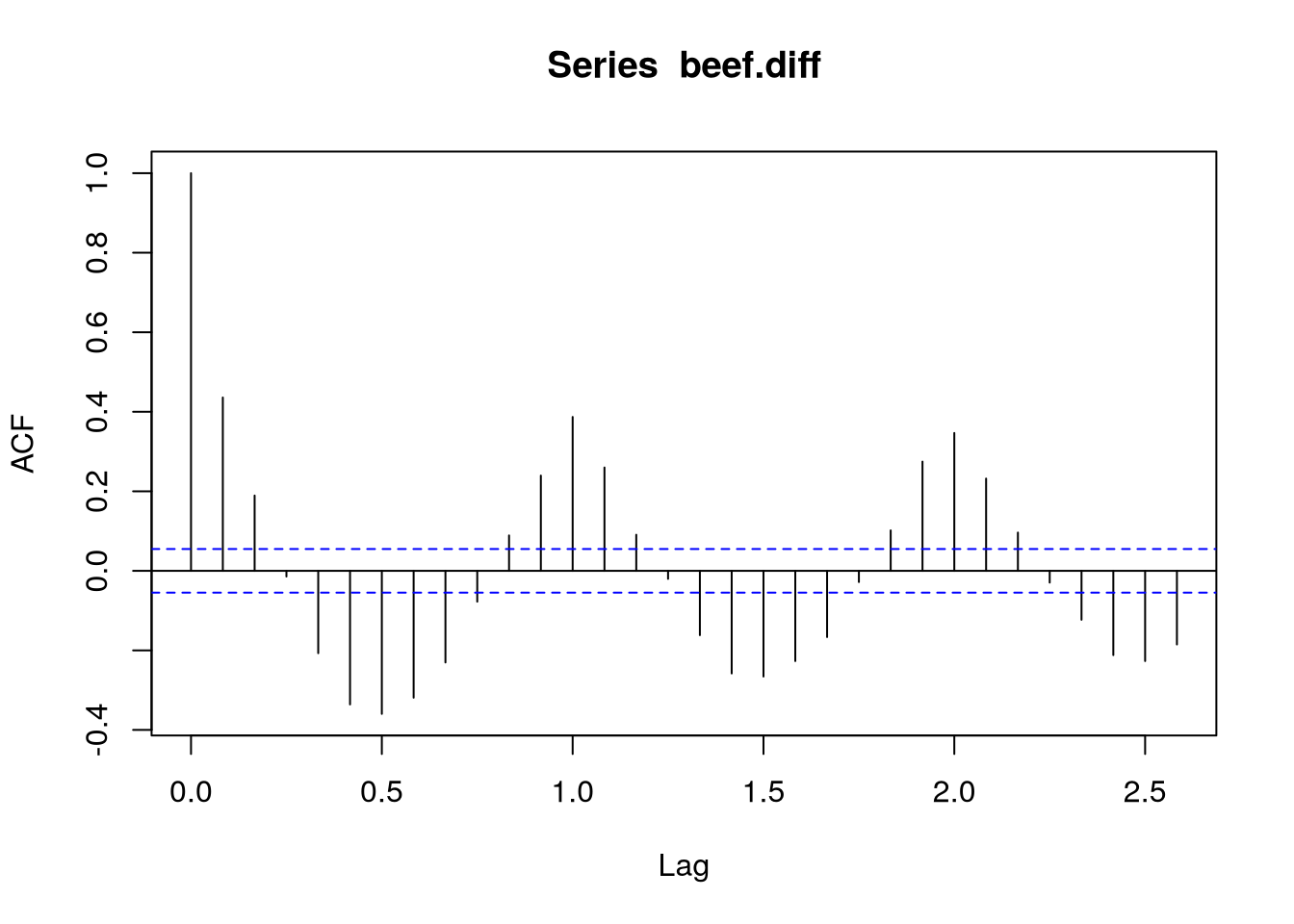
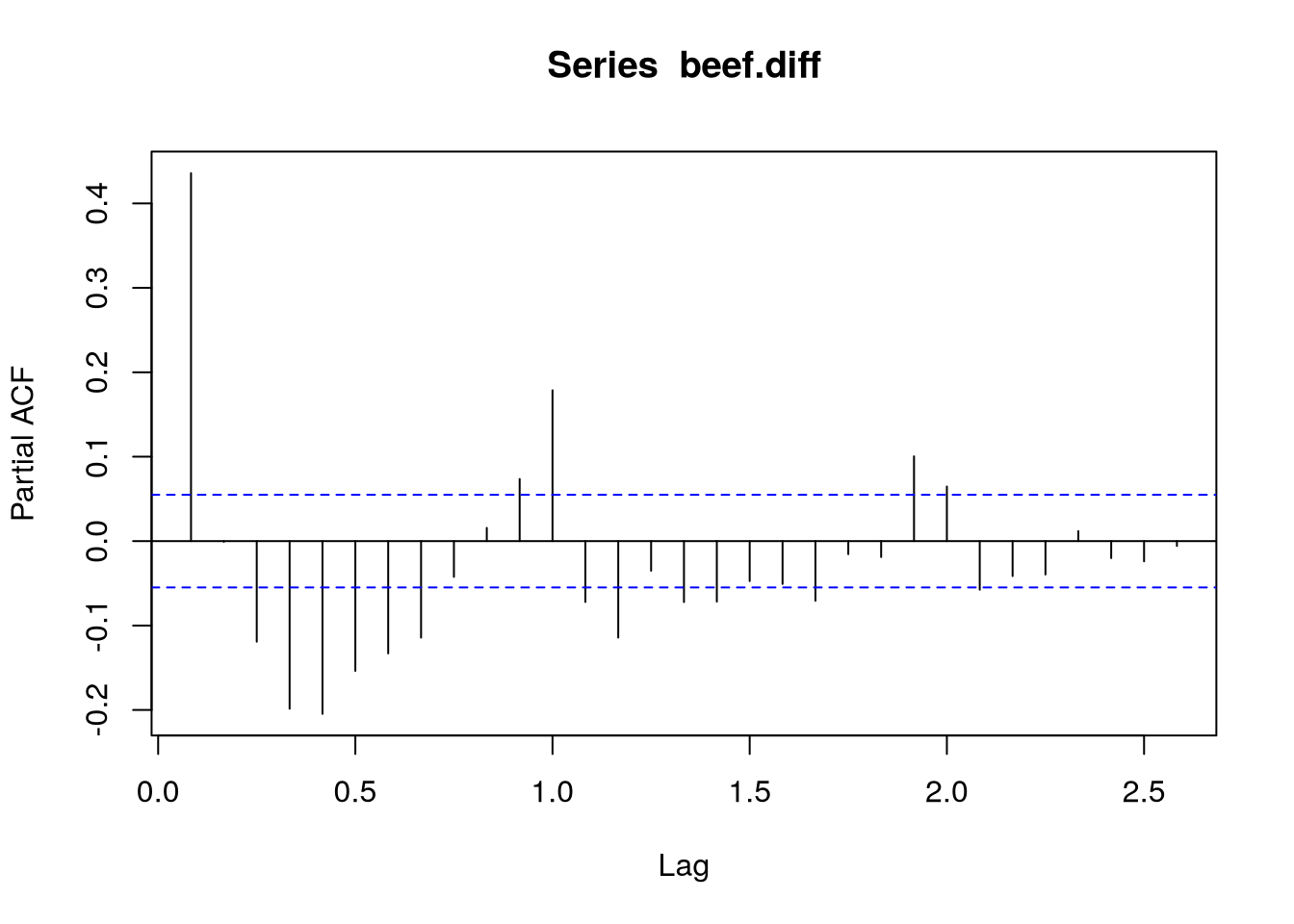
Po prvním diferencování a vykreslení autokorelační funkce, viz Obrázek 1, vidíme, že tato transformace neodstraní autokorelační strukturu. Konkrétně si můžeme všimnout silné sezónní složky projevující se negativní autokorelací po šesti měsících,
Použijeme-li dále diferenci se zpožděním 12, povede se nám odstranit sezónnost, čehož si můžeme povšimnout vykreslením autokorelační funkce \(\rho\), případně pak i PACF \(\alpha\), viz Obrázek 2.
beef.year.diff <- diff(beef.diff,
lag = 12)
plot(beef.year.diff)
acf(beef.year.diff)
pacf(beef.year.diff)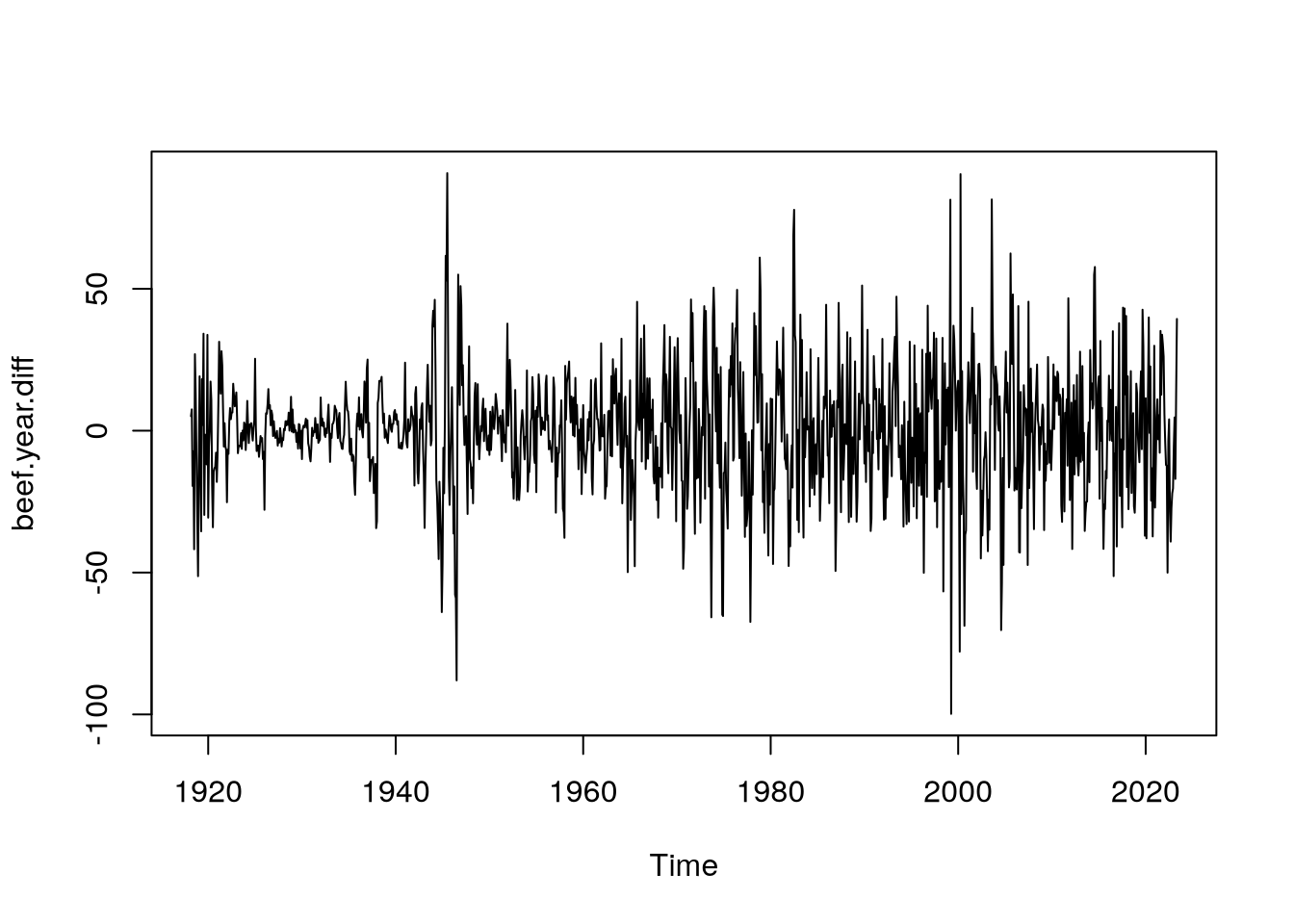
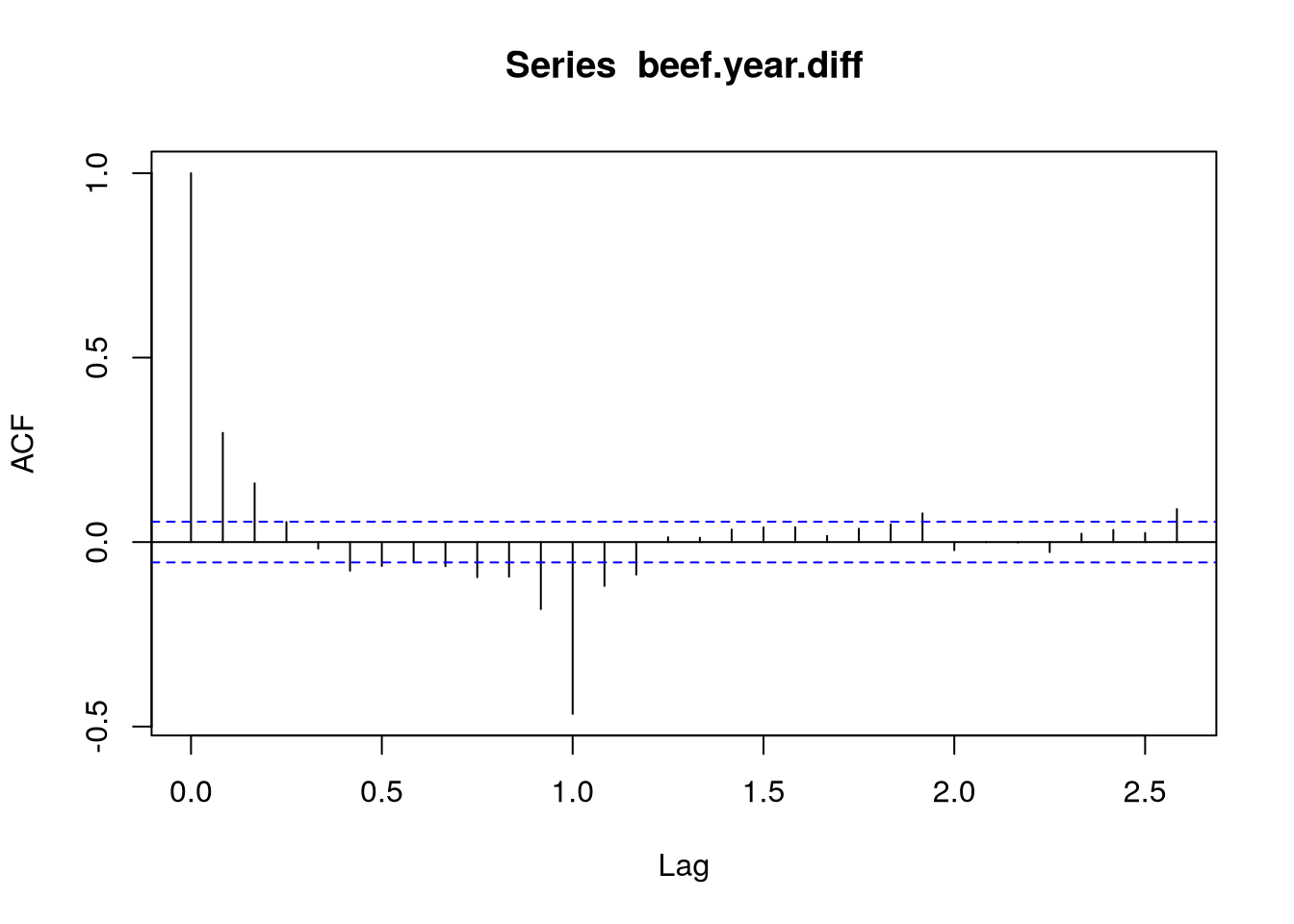
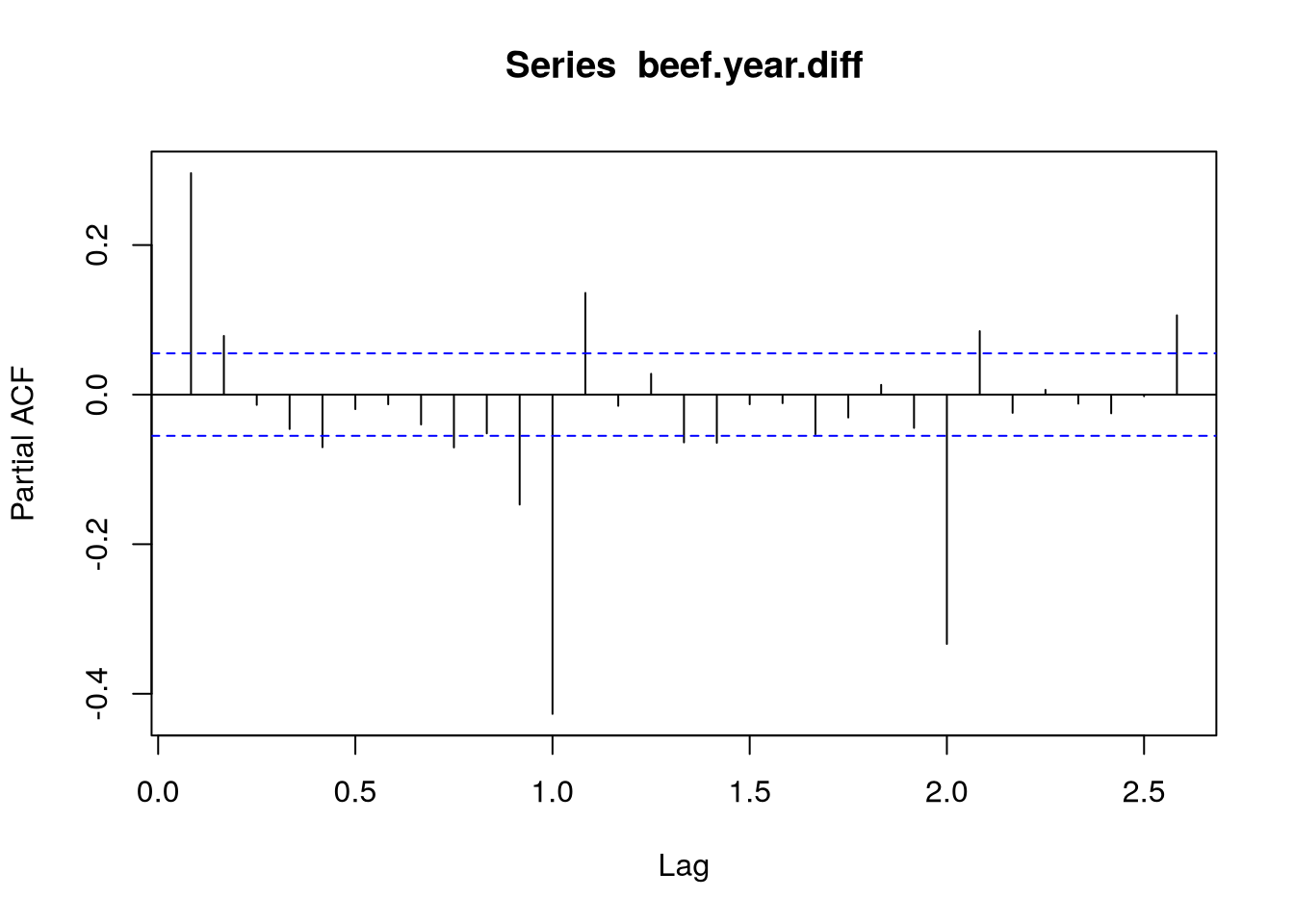
Dále si na Obrázek 2 povšimněme, že ani na ACF, tak na PACF nepozorujeme náhlý pokles, spíše pak obě funkce vykazující exponenciální tlumení. To nám naznačuje, že bude potřeba použít jak autoregressní složku, tak i složku klouzavého průměru ARMA, resp. v našem případě dokonce SARIMA, modelu.
Dalším krokem analýzy byla dekompozice časové řady. Pomocí funkce stl jsme rozdělili naše data na složku trendovou, sezónní a zbytkovou.
plot(stl(beef.data,
s.window = 12))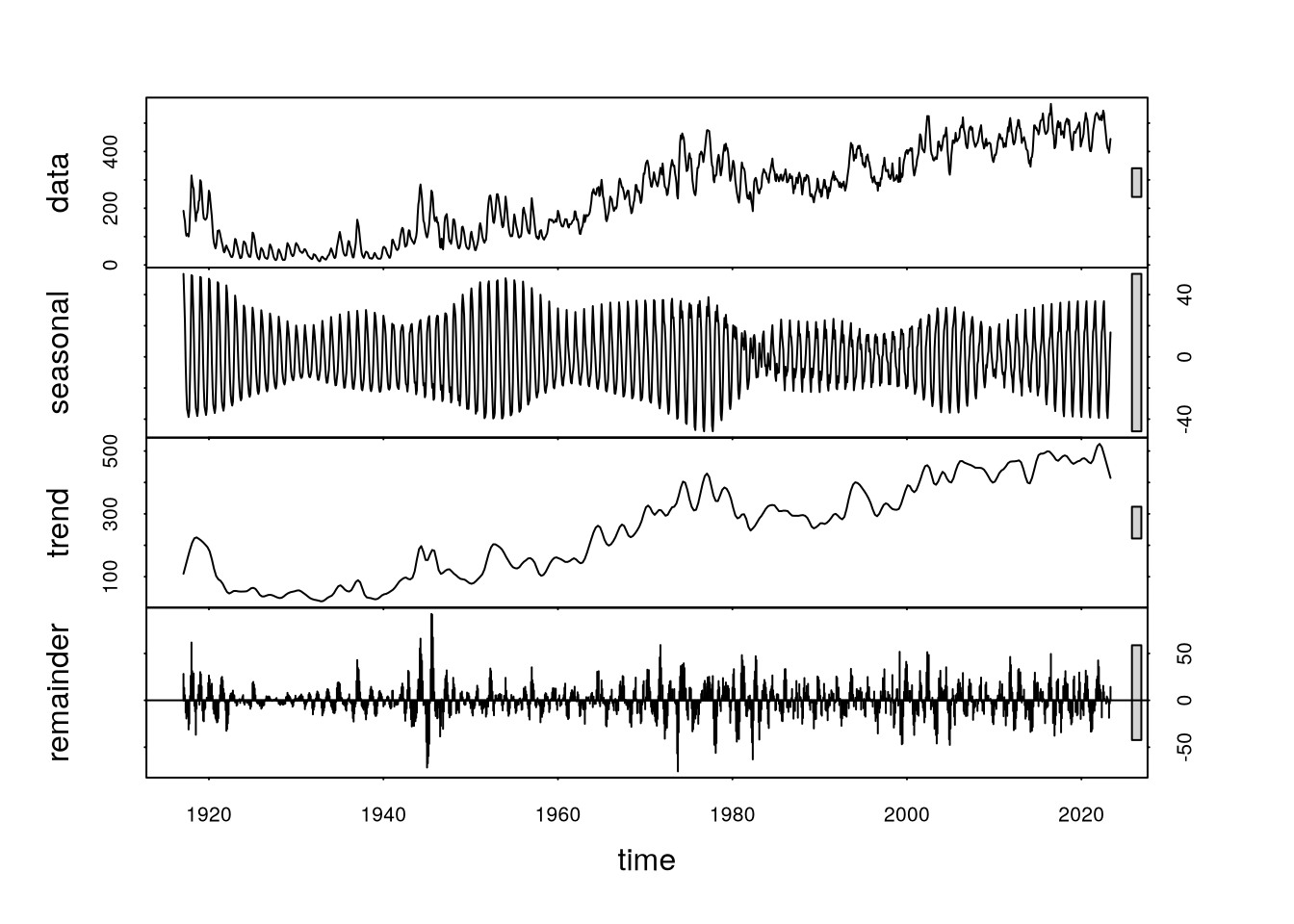
stlNa Obrázek 3 vidíme cyklickou sezónní složku a mírně rostoucí trend. V období kolem roku 1960 si můžeme všimnout výraznějšího nárůstu trendové složky. Tuto skutečnost si vysvětlujeme tím, že právě kolem roku 1960 došlo k významnému rozšíření velkých komerčních výkrmných stanic a proto se chov hovězího masa začal rychle rozšiřovat, viz Peel (2022).
Další možností dekompozice bylo využít aditivní dekompozici pomocí funkce decompose, která stejně jako stl rozloží časovou řadu na trendovou, sezónní a zbytkovou složku. V případě decompose je ale odhadnutá sezónní složka sice periodická, ale s konstantní amplitudou, což nám vzhledem k charakteru dat nepřijde příliš šťastné, viz Obrázek 4. Vhodnější bude dekompozice pomocí funkce stl.
plot(decompose(beef.data,
type="additive"))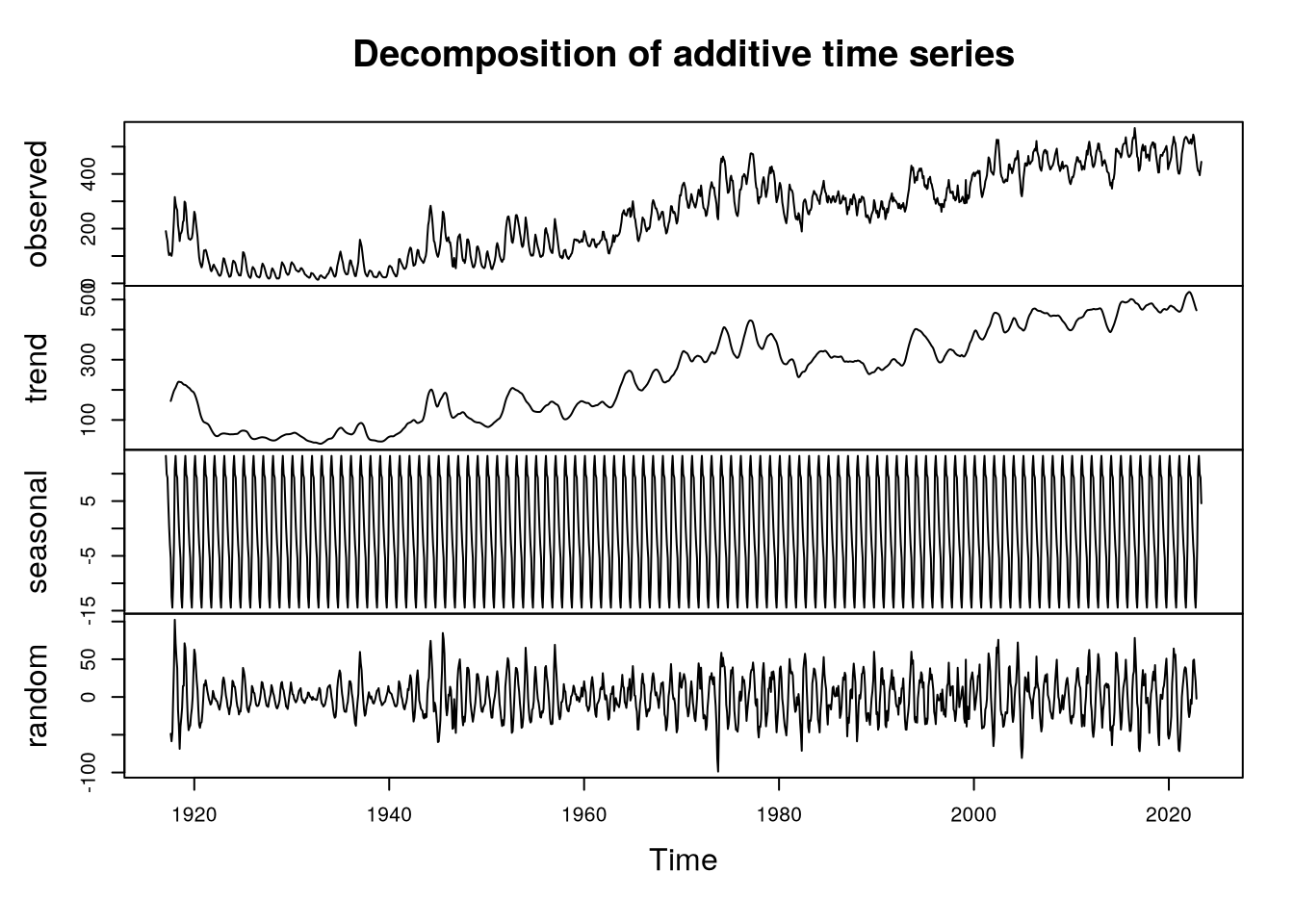
decomposePomocí Holt-Wintersovy metody jsme odhadli prvotní model a predikci naší časové řady – jedná se o exponenciálně vážený klouzavý průměr.
# we let alpha, beta, gamma be selected automatically
m = HoltWinters(beef.data)Dále jsme pomocí funkce predict vypočítali predikci včetně predikčních intervalů na 24 měsíců dopředu. Tuto situaci vidíme znázorněnou na Obrázek 5.
p = predict(m, 24,
prediction.interval=TRUE)
plot(m, p,
main="")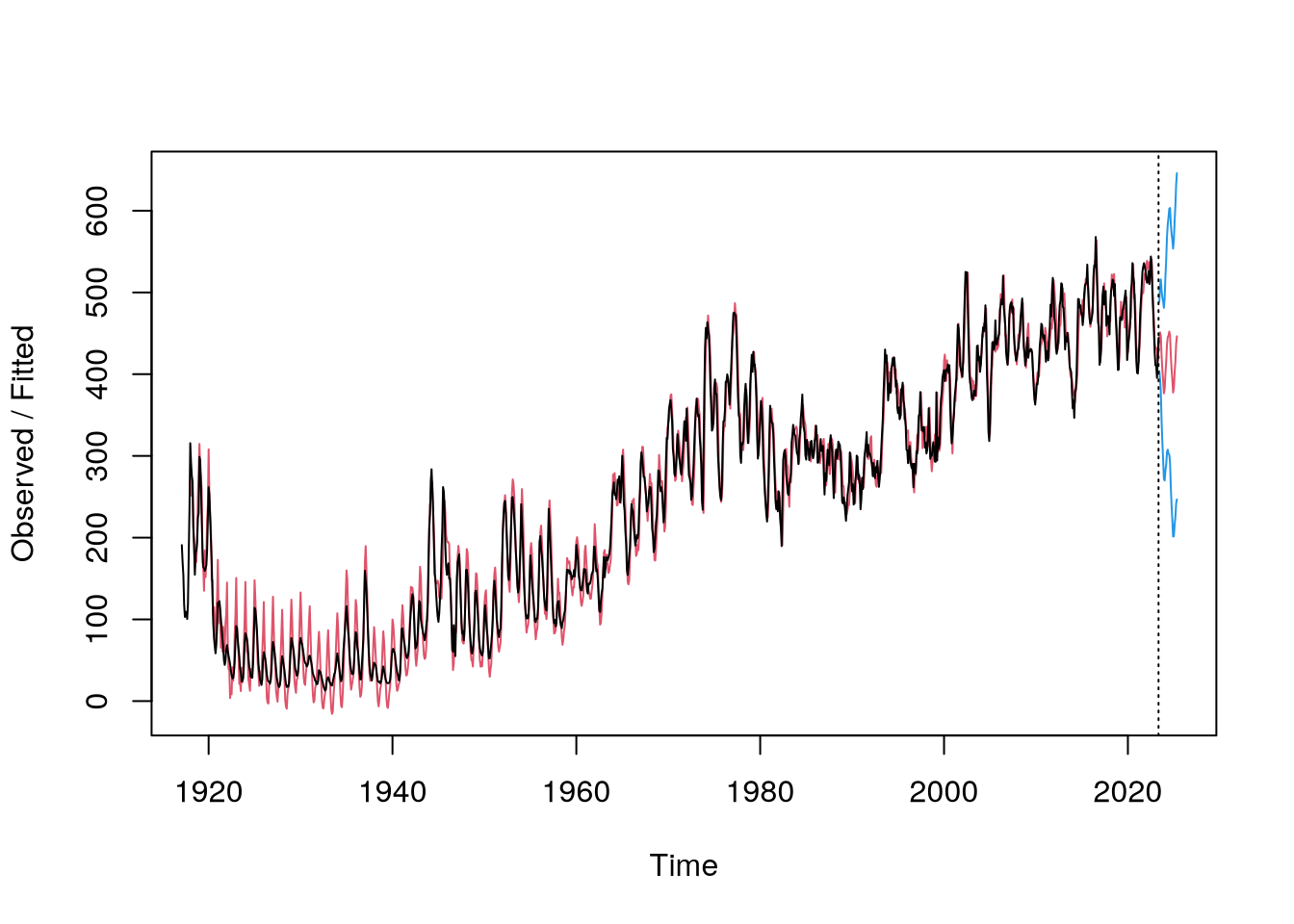
Jak je vidět z dřívější výpočtů, hlavně pak z Obrázek 2, v našem modelu budeme potřebovat nejen meziměsíčně diferencovat, ale i zohlednit sezónost pomocí druhé, tentokrát roční, diference. Aplikováním funkce tsdisplay z balíčku forecast na tuto řadu můžeme vidět klasickou a parciální autokorelační funkci, viz Obrázek 6, na čemž můžeme zkontrolovat naše závěry.
tsdisplay(beef.year.diff)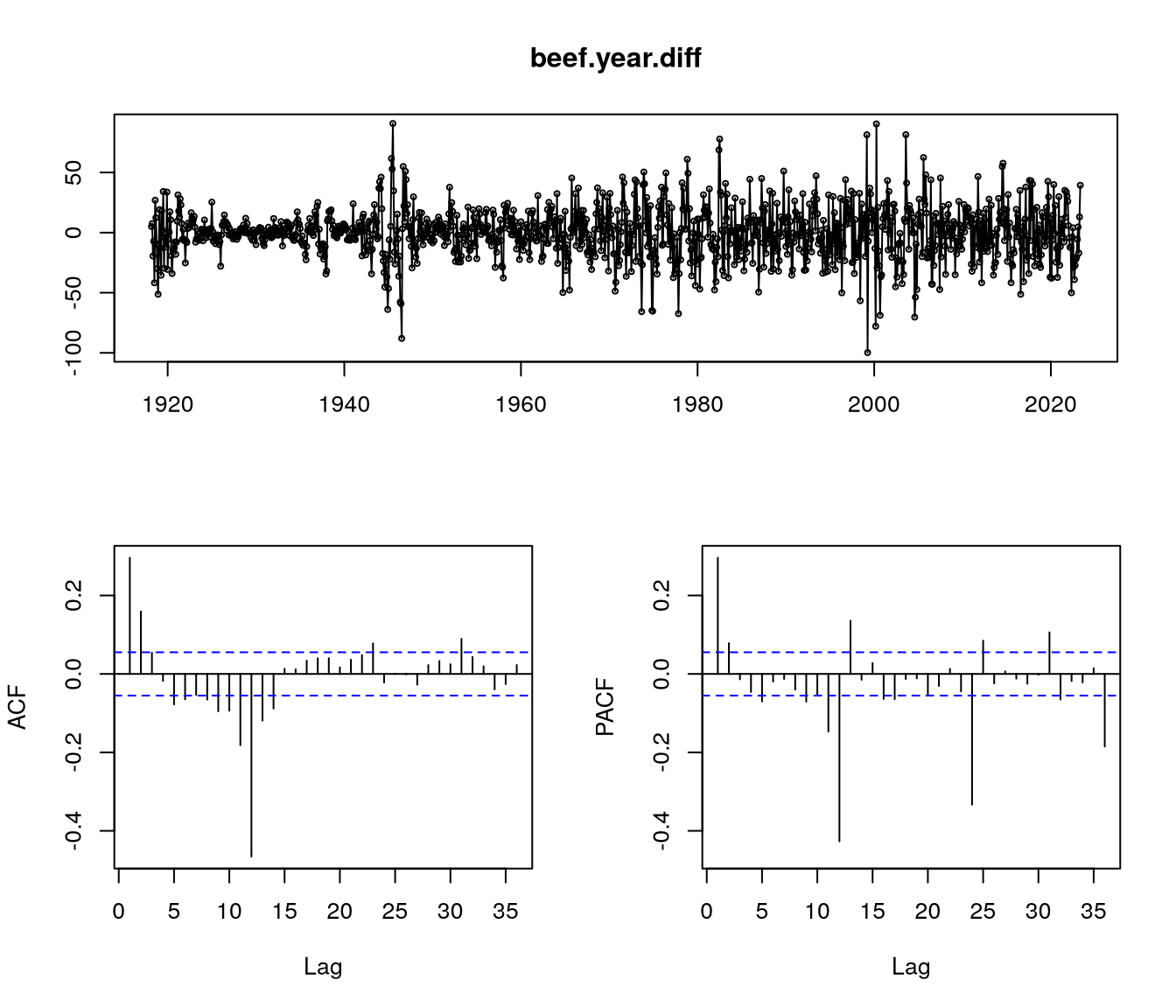
Jelikož u ACF i u PAFC vidíme exponenciální pokles, předpokládáme, že nejvhodnější bude použít model zahrnující jak klouzavé průměry, tak autoregresi.
Z důvodu přítomnosti sezónnosti v našich datech jsme se rozhodli využít SARIMA model. Po návrhu pár modelů nám nejlépe vyšly dva, a to konkrétně \(\mathrm{ARIMA}\left( 2,1,2 \right)\left( 1,1,2 \right)_{12}\)
beef.arima.best <- arima(beef.data,
order = c(2,1,2),
seasonal = c(1,1,2))
tsdiag(beef.arima.best, gof.lag = 15)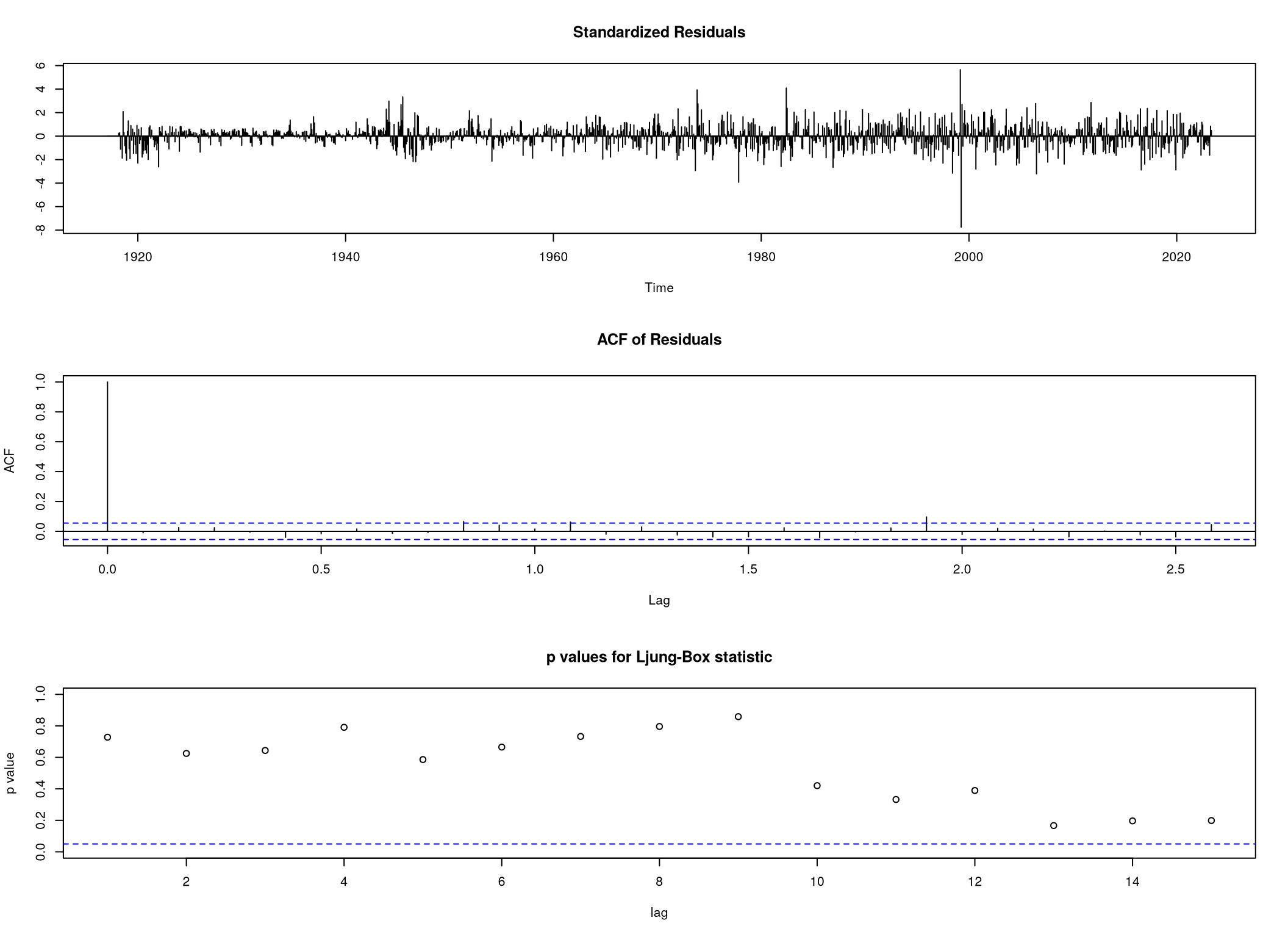
a složitější \(\mathrm{ARIMA}\left( 2,1,2 \right)\left( 2,1,2 \right)_{12}\)
beef.arima.nonconv <- arima(beef.data,
order = c(2,1,2),
seasonal = c(2,1,2))
tsdiag(beef.arima.nonconv, gof.lag = 15)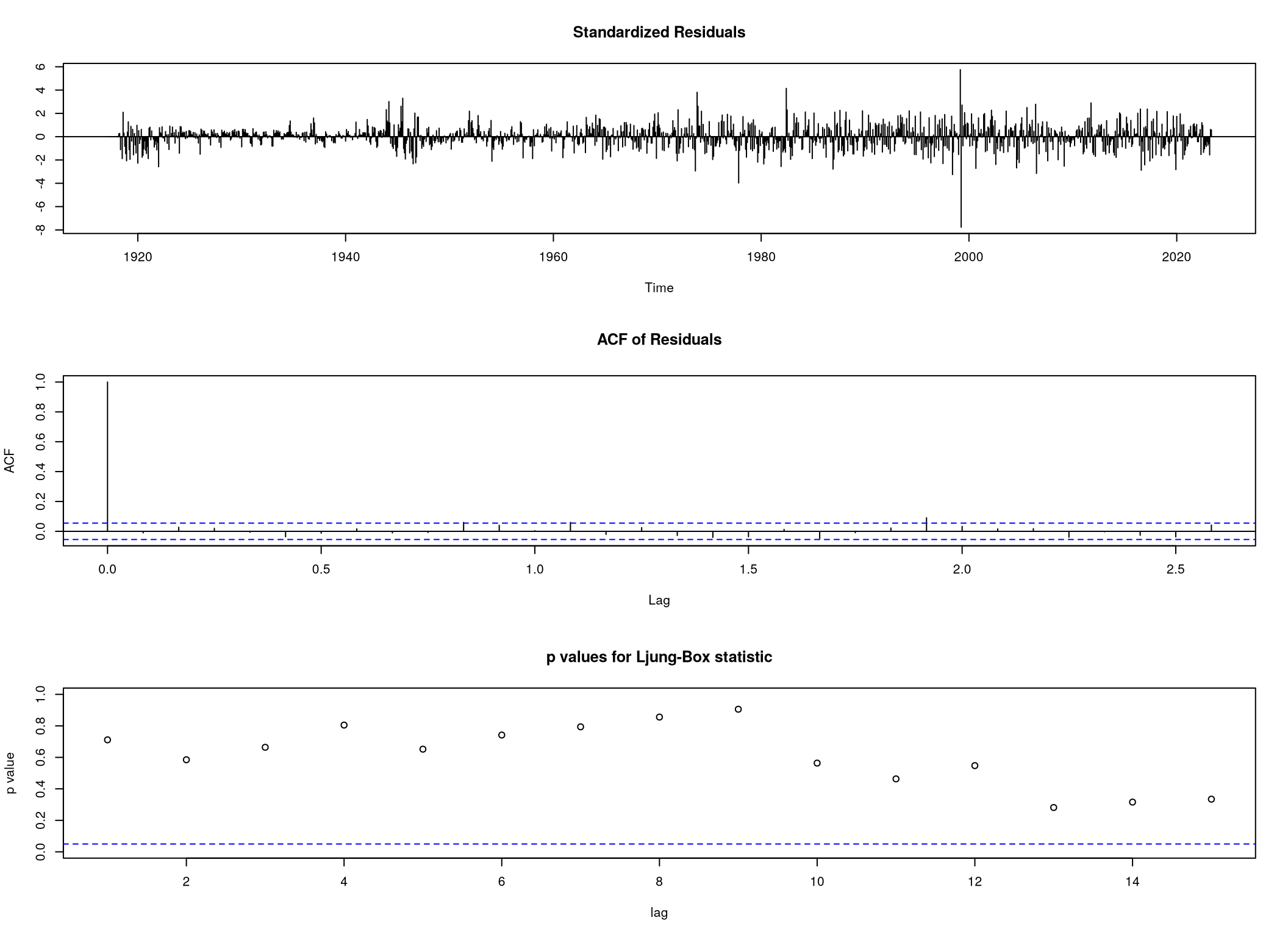
Při konstrukci druhého modelu má R potíže s konvergencí u optimalizační metody zajišťující výběr parametrů. I kvůli tomuto možnému problému jsme se rozhodli otestovat, zda by nebylo možné odstranit sezónní autoregresní složku řádu 2.
Využitím testu podílu log-věrohodnosti jsme zjistili, že je opravu možné považovat parametr sar2 za nulový.
L <- 2 * (beef.arima.nonconv$loglik - beef.arima.best$loglik)
pvalue <- 1 - pchisq(L, 1)Dále budeme proto uvažovat model beef.arima.best. R nabízí i funkci auto.arima, která by měla najít nejlepší model jednorozměrné časové řady. Zkusili jsme s její pomocí vytvořit model beef.auto přes
beef.auto <- auto.arima(beef.data)a porovnat jej s naším modelem
AIC(beef.auto)[1] 10617.23AIC(beef.arima.best)[1] 10473.4Oba dva modely mají stejný počet parametrů, dává tedy smysl jako hodnotící kritérium použít Akaikeho informační kritérium. Jak vidíme, AIC(beef.auto) > AIC(beef.arima.best), proto budeme i nadále uvažovat pouze námi navržený model.
Další částí je analýza reziduí našeho modelu.
res <- beef.arima.best$residuals
plot(res)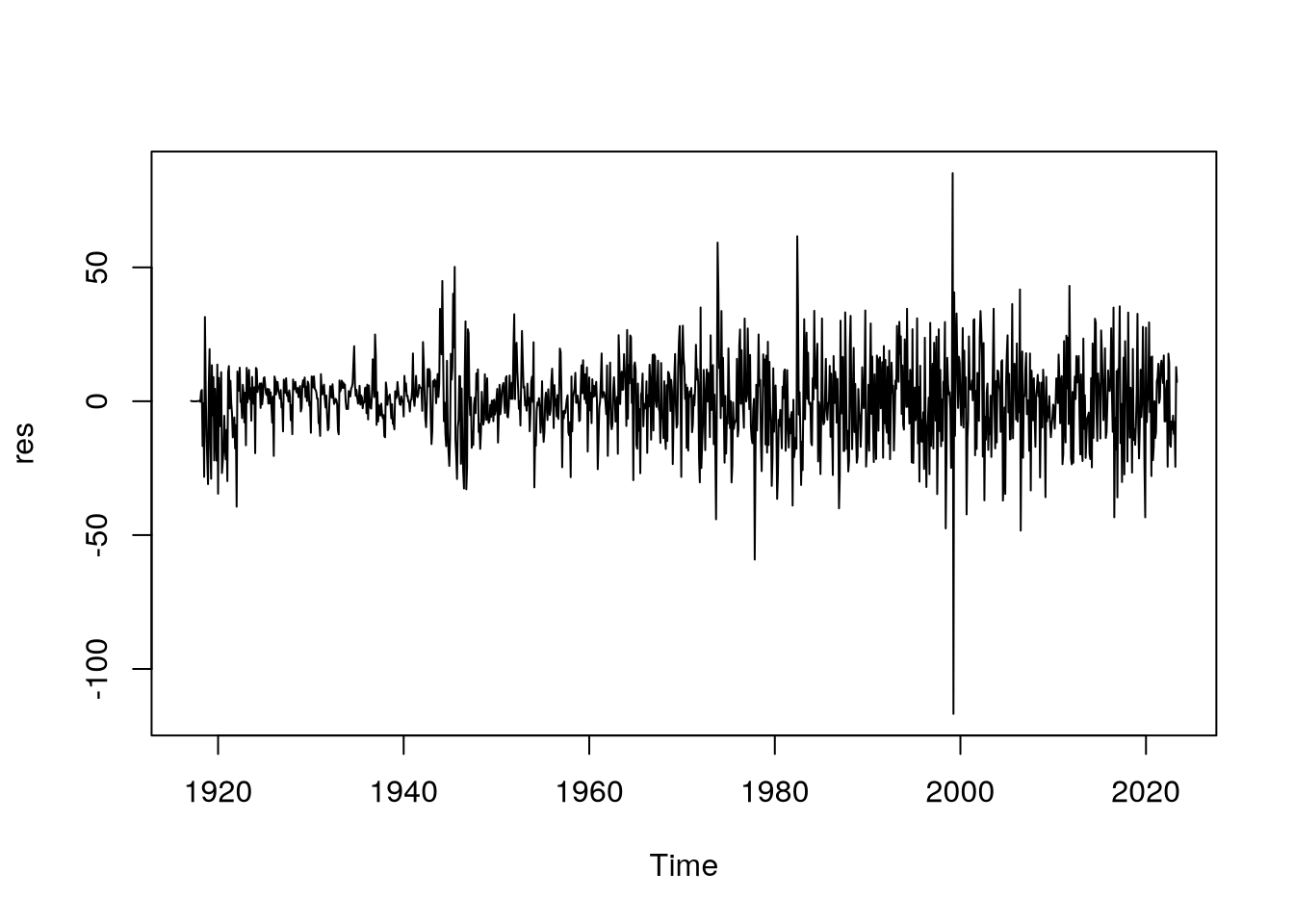
Po jejich extrahování z modelu a následného vykreslení vidíme, že až na pár odlehlých pozorování se rezidua chovají normálně. Jejich normalitu ověříme i pomocí QQ-plotu. Na Obrázek 9 vidíme, že oprávněně můžeme předpokládat, že rezidua jsou normálně rozdělena.
qqnorm(res)
qqline(res)
hist(res)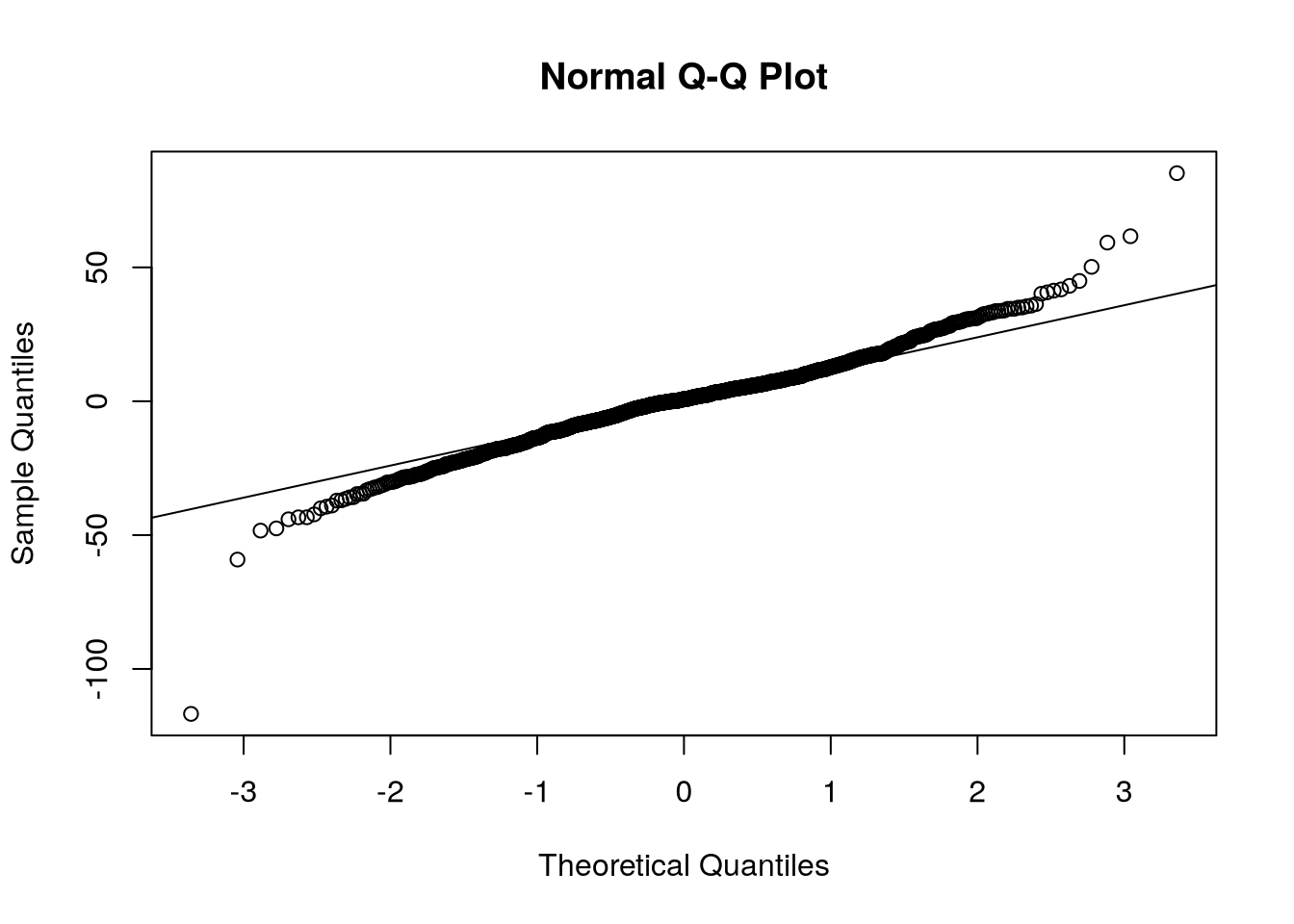
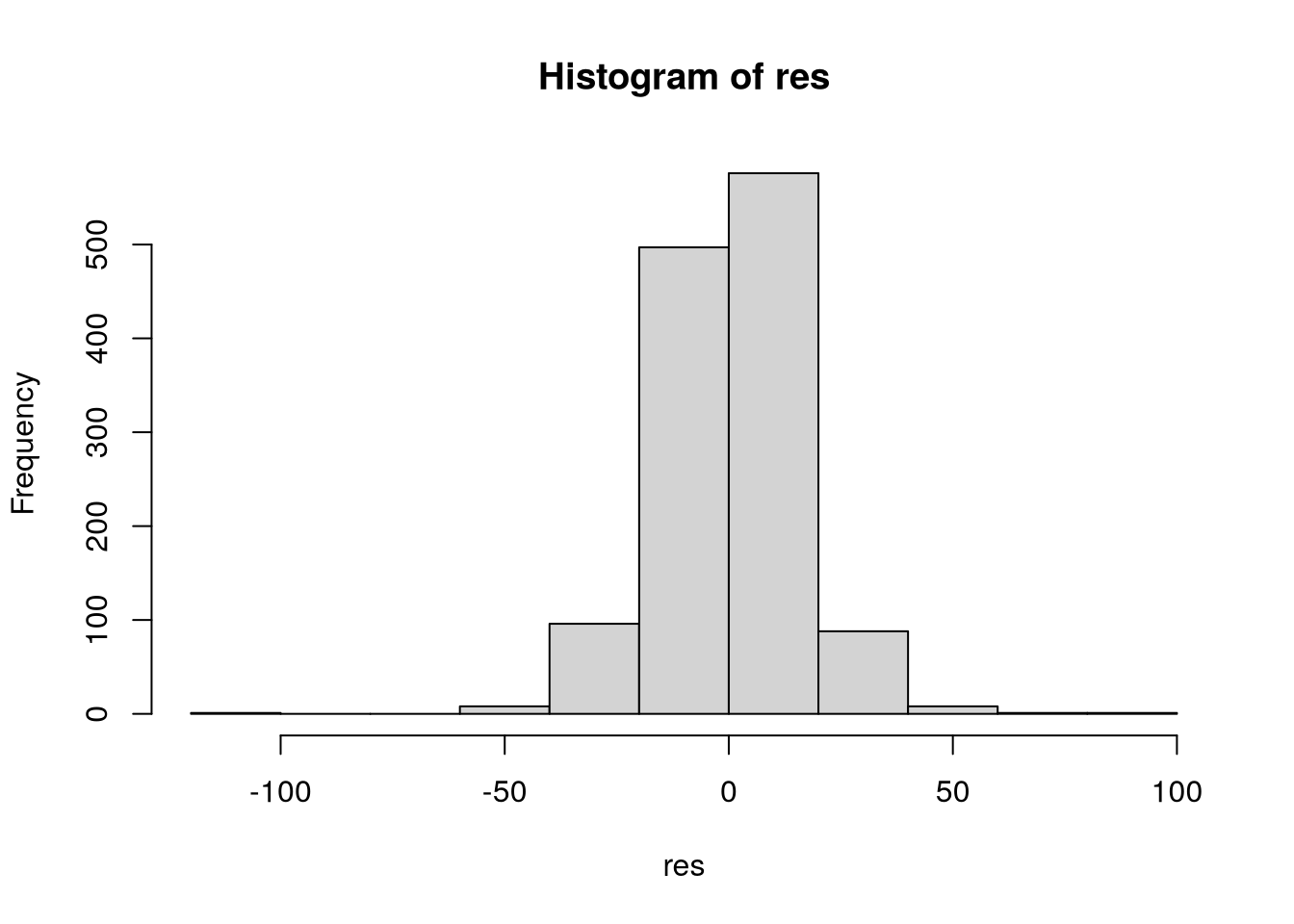
Dále (například jednovýběrovým \(t\)-testem) nemůžeme zamítnout hypotézu, že střední hodnota reziduí je rovna nule.
t.test(res, mu = 0)
One Sample t-test
data: res
t = 0.43699, df = 1275, p-value = 0.6622
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-0.6402816 1.0072634
sample estimates:
mean of x
0.1834909 Navíc z funkce tsdiag vidíme, viz Obrázek 10, že rezidua jsou nekorelovaná.
tsdiag(beef.arima.best)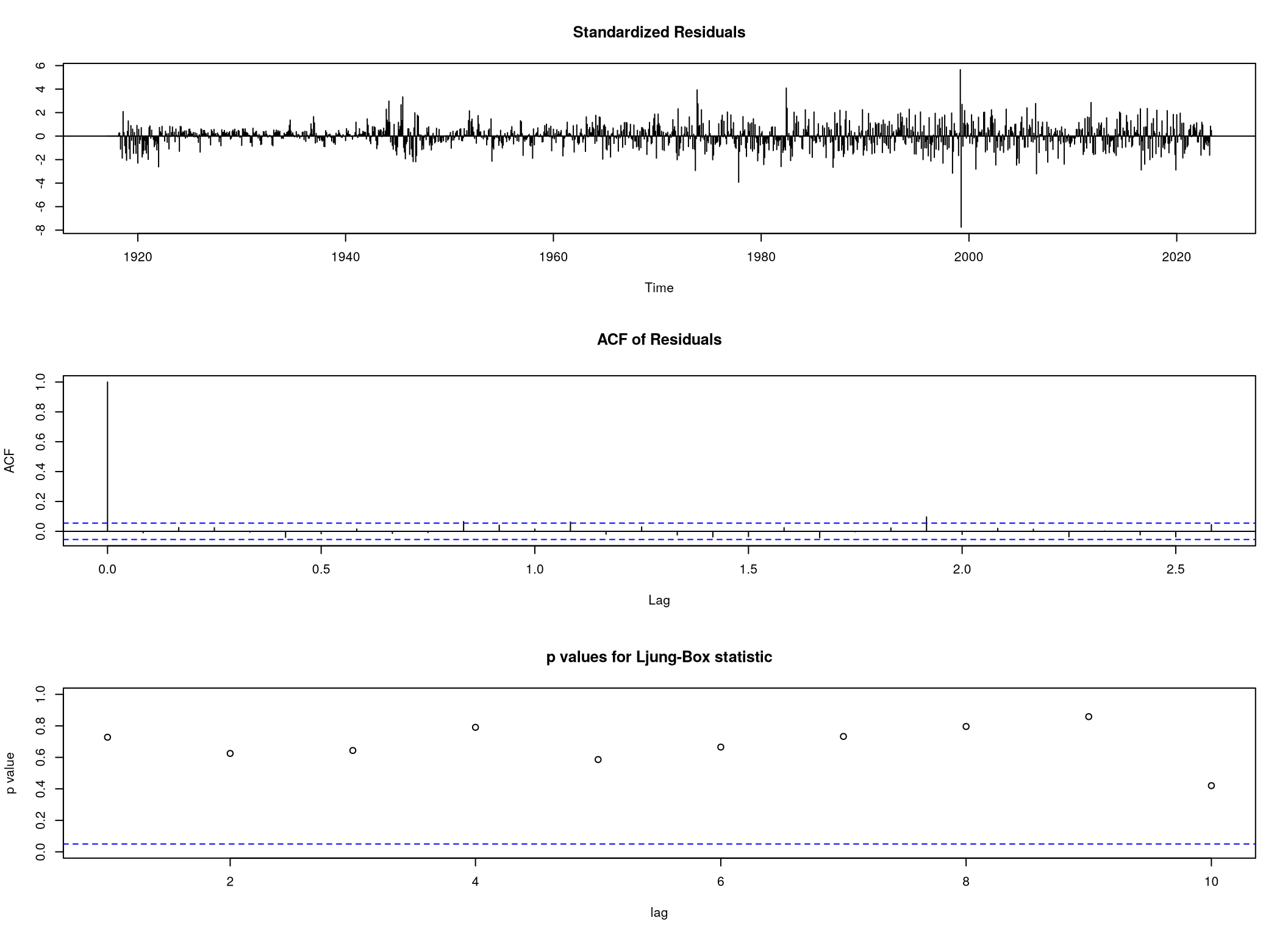
Na závěr našeho projektu se pokusíme predikovat budoucí hodnoty množství hovězího masa uskladněného ve veřejných a soukromých chladírenských skladech.
Pomocí funkce forecast, opět z balíčku forecast, můžeme predikovat budoucí hodnotu na následující tři roky, tedy 36 měsíců.
beef.predict <- Arima(beef.data,
order = c(2,1,2),
seasonal = c(1,1,2))
beef.forecast <- forecast::forecast(beef.predict,
h = 36)Následně vykreslíme celý graf, viz Obrázek 11, a vidíme, že v posledních pěti letech hodnoty spíše stagnují, možná dokonce i mírně klesají. To se projeví i naší predikci.
plot(beef.forecast)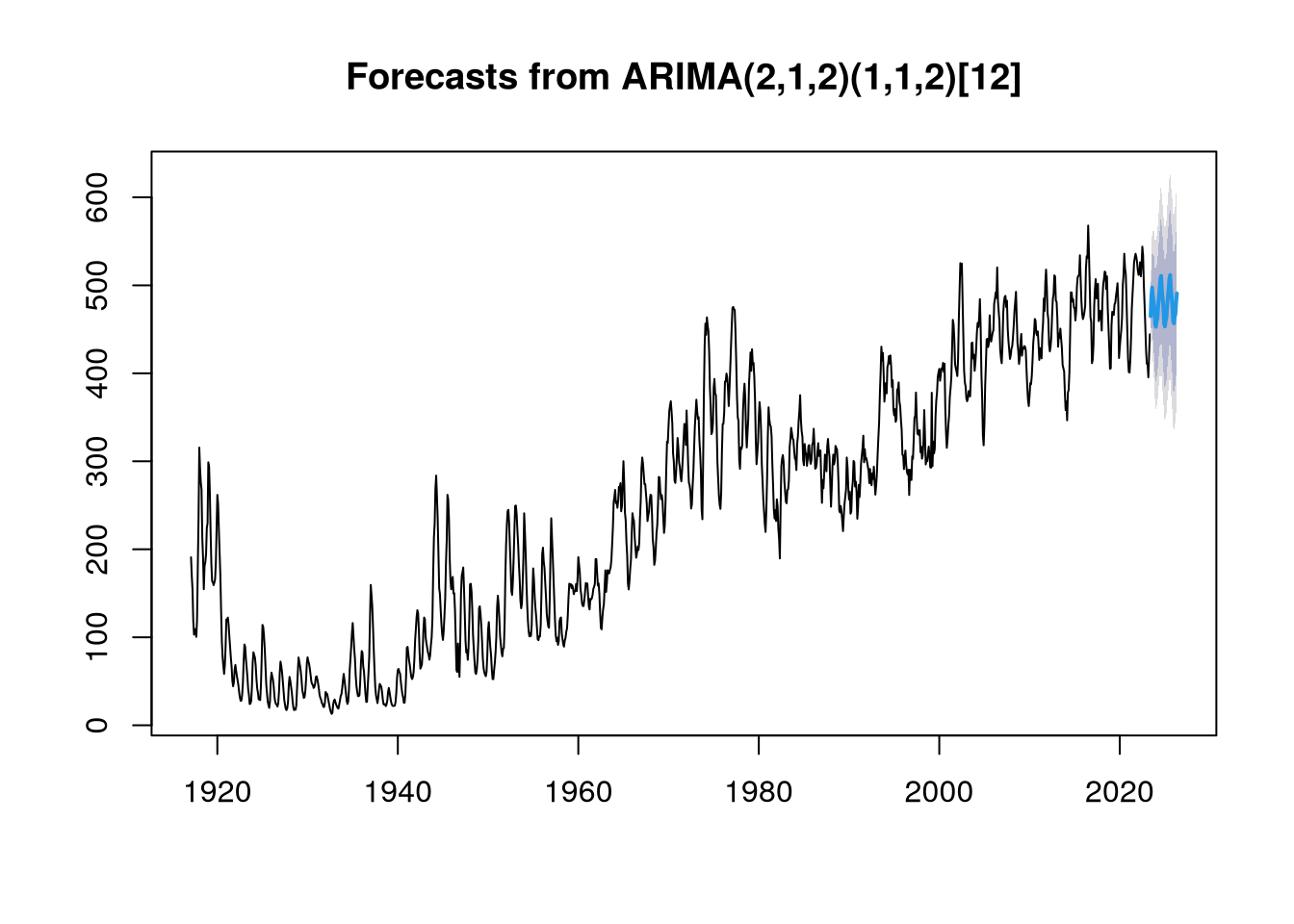
Vysvětlení stagnace, případně mírného poklesu, může být vícero. Jedno se přímo nabízí. V poslední dekádě se poměrně výrazně ve vyspělých zemích řeší enviromentální otázka a produkce hovězího masa je poměrně významný producent metanu a dalších skleníkových plynů. Proto jsme dospěli k jednoduchému závěru: MOHOU ZA TO VEGANI!!!